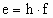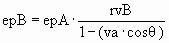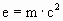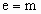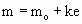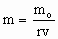Relationship between a body's absolute velocity and its wave/particle energy and mass
     A body in reference frame B of Fig. 1 has a mass that is greater than its mass when at rest in the qm. This is a consequence of various influences on the body's wave/particle energy which comprises the body's total mass/energy.
     Assume that in Fig. 1 photons are exchanged between an atom at the origin of A and an atom at the 1 ls location on the x axis, and that the same exchange of photons is occurring between atoms of the same element in B. Assume that at every .2 s on an origin clock, a photon is emitted toward the 1 ls location where the photon is absorbed, and that whenever a photon is absorbed at the 1 ls location in A or B, another photon is immediately emitted back toward the origin. At any time in reference frame A there will be 5 photons moving toward Ax=1 and 5 photons moving toward Ax=0, as shown in Figure 4. The photons moving along the x axis are represented by arrows next to the axis so they can be seen. A photon is at the tail end of an arrow and an arrow's length is proportional to the photon's velocity relative to the reference frame.
     The total energy of the 10 photons moving along the Ax axis depends on the oscillation frequency of the photons according the Planck-Einstein relationship as follows (where e is the photon energy, h is the Planck constant, and f is the oscillation frequency).

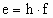(22)

In A all the photons are observed to have a certain frequency, and in B all the photons are observed to have this same frequency (because in B the atoms' emission frequency is rvB times the frequency in A and the rate of clocks in B is rvB times the rate in A).
     The total energy of the 10 photons moving along the x axis of reference frame B is greater than the energy in A for various reasons. Photons emitted in B in the direction of va are Doppler blueshifted which increases their energy by a factor of 1/.4 or 2.5. Photons emitted back toward the origin are redshifted by a factor of 1/1.6 or .625. The ratio of the energy of a blueshifted photon to the energy of a redshifted photon is 4, the asymmetry ratio (N), which is a function of the absolute velocity, va, of the reference frame as follows.

(23)

     The blueshifted photons move along the x axis with a velocity of .4 ca relative to B, and take 2 sa to arrive at Bx=1 which is .8 LS from Bx=0. The redshifted photons move along the x axis with a velocity of 1.6 ca relative to B, and take only .5 sa to arrive at Bx=0. As shown in Fig. 4, 8 blueshifted photons are moving toward Bx=1 and only 2 redshifted photons are moving toward Bx=0. This results in a net gain in energy of the photons moving along the x axis due to the absolute motion of B through the qm. Due to the absolute motion of B, photons arrive at Bx=1 at the same rate as at Bx=0, and in B all the photons appear to have the same energy due to the Doppler redshifts when the photons are absorbed at Bx=1 and blueshifts when photons are absorbed at Bx=0. Therefore, observers in B do not detect the asymmetries in the energies and quantities of the photons moving along the x axis.
     Let epA be the energy of each photon moving along the x axis of A. Therefore, in A the total energy of the 10 photons moving along the Ax axis is 10 epA. In B the emission frequency prior to Doppler shifting is rvB times the emission frequency in A due to the slowing of all processes in B. Therefore, the total energy of the 8 blueshifted photons moving toward Bx=1 is (8·.8/.4) epA or 16 epA, and the total energy of the 2 redshifted photons moving toward Bx=0 is (2·.8/1.6) epA or 1 epA. Therefore, the ratio of the total energy of the photons moving along the x axis in B to the total energy of the photons moving along the x axis in A is 1.7, even though the observed photon energy and spacing along the x axis is the same in both reference frames.
     Figure 4 also shows photons traveling along the z axes of A and B. These photons were also emitted at .2 s intervals on the clocks in these reference frames. Because A is at rest in the qm, the total energy of the 10 photons traveling along the Az axis is the same as along the Ax axis. In B, the 10 photons traveling along the Bz axis must have a +x direction component of their 1 ca velocity through the qm equal to .6 ca. Therefore, the velocity of the photons along the Bz axis is .8 ca as shown. These photons must be moving through the qm at an angle of 53.13° to the Bx axis. The energy of these photons is affected by the lower emission frequency in B and by the Doppler shift at emission as follows.

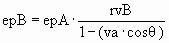(24)

When θ=53.13°, epB=1.25 epA. Therefore, the total energy of the 10 photons moving along the Bz axis is 1.25 times the energy of the 10 photons moving along the Az axis.
     Following this same procedure for comparing the total energy of the photons moving along the x and z axes in B to the energy in A, we could do the same along other lines that pass through the origin of the reference frame and are in the xz plane. We could determine the total internal wave/particle energy being exchanged within a body in B compared with its total internal energy when it is brought to rest in the qm and reference frame A. This is somewhat complicated and it will not be included in this discussion. It was found that a body's internal energy is just sufficient to account for its kinetic energy and its observed inertia if it is assumed that a body's observable mass is a consequence of its internal wave/particle energy.
     This assumption, that a body's mass is a consequence of its internal energy, is consistent with Einstein's equation relating a body's energy and mass.

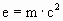(25)

When the speed of light is used as the unit of velocity (as in the qm view) Eq. (25) is as follows.

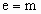(26)

The basic unit of mass and energy is the absolute kilogram (kga), 1 kg of matter at rest in the qm. In the quantum medium view, a body's kinetic energy (ke) is the energy that the body can supply in the process of being brought to rest in the qm. A body moving through the qm has a mass (m) that is the sum of it's at-rest mass (m_o) and its kinetic energy, ke, as follows.

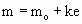(27)

A body's mass, m, is also related to its at-rest mass and physical change ratio as follows.

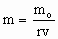(28)

Equations (27) and (28) are consistent with experimental evidence, as will become more apparent in the following discussion.