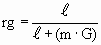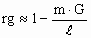|
Premise II
In the quantum medium view, the observed gravitational attraction between bodies
is a consequence of the following premise.
Premise II: A massive body (or other
concentration of mass/energy) has an effect on the quantum medium which decreases the speed
at which wave/particle energy (e.g. light) is propagated through the medium.
|
Presumably a massive body affects the permittivity and permeability of the qm so that the
speed of light specified by Eq. (4) is decreased. Possibly massive bodies and other
concentrations of mass/energy emit a radiation into the qm which slows the speed of light
through the medium. We will assume that massive bodies emit such photon slowing
radiation. Therefore, in the vicinity of a massive body the speed at which wave/particle
energy is propagated through the qm (cag) is less than ca.
The slowing of the speed of wave/particle energy through the
qm decreases the energy exchange rate in a reference frame or body, similar to the decrease
in energy exchange rate caused by the motion of a reference frame or body through the qm. As
discussed above, the ratio of a body's energy exchange rate when moving through the qm
to its at-rest rate is equal to the body's physical change ratio, rv. Similarly, where the
speed of light in the qm is cag, the physical change ratio (rg) is the ratio of the
energy exchange rate to the rate where the speed of light is ca.
The physical change ratio, rg, for a location in the qm affected
by a massive body is a function of the mass (m) of the massive body, the distance
(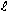 ) from the center of mass of the massive body, and
the universal gravitational constant (G) as follows. ) from the center of mass of the massive body, and
the universal gravitational constant (G) as follows.
| | 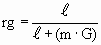 |
(33) |
Mass, m, is in kilograms. When distance, 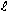 , is in LS units,
G is 2.47·10-36. Therefore, at Earth's surface, rg due to
Earth's mass is approximately .999999999305 because Earth's mass is about
5.98·1024 kga and Earth's radius is
about .021266 LS. , is in LS units,
G is 2.47·10-36. Therefore, at Earth's surface, rg due to
Earth's mass is approximately .999999999305 because Earth's mass is about
5.98·1024 kga and Earth's radius is
about .021266 LS.
When rg is close to 1 (as on Earth where rg due to the masses
of Earth, Sun, and the rest of our Galaxy is close to 1), rg is closely approximated
by Eq. (34).
| | 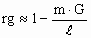 |
(34) |
Even if Earth's mass were ten million times its present mass, rg on Earth via Eq. (34)
would be close to rg via Eq. (33) (.99300 and .99305 respectively). Only in cases of
exceptionally large masses combined with small distances (e.g. around a neutron star) does
Eq. (34) not give good approximations of rg. Because Eq. (34) can yield rg<0, which
is equivalent to qm environments where the speed of light and the rate of energy exchange
are negative, it is not consistent with logic. Although Eq. (33) does not predict black
holes, it does predict dark attractors that would emit only very weak radiation and would
cause gravitational lensing.
|
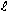 , is in LS units,
G is 2.47·10-36. Therefore, at Earth's surface, rg due to
Earth's mass is approximately .999999999305 because Earth's mass is about
5.98·1024 kga and Earth's radius is
about .021266 LS.
, is in LS units,
G is 2.47·10-36. Therefore, at Earth's surface, rg due to
Earth's mass is approximately .999999999305 because Earth's mass is about
5.98·1024 kga and Earth's radius is
about .021266 LS.