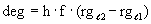|
Gradients of rg and physical causes of gravity
Figure 7 shows a
laboratory at rest in the qm one Earth radius away from a massive body of one Earth mass.
The laboratory is 300 ma or 10-6 LS high as shown.
The bottom of the lab is 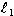 =.021266 LS from the massive body and the top
of the lab is =.021266 LS from the massive body and the top
of the lab is 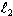 =.021266+10-6 LS
from the massive body. Therefore, a gradient of rg exists in the lab. Using Eq. (33) and
the above values for =.021266+10-6 LS
from the massive body. Therefore, a gradient of rg exists in the lab. Using Eq. (33) and
the above values for 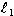 , , 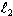 , m, and G, rg at the
bottom of the lab is , m, and G, rg at the
bottom of the lab is 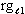 =.9999999993054359 and rg at the top of the
lab is =.9999999993054359 and rg at the top of the
lab is 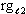 =.9999999993054685. Throughout the lab, energy is being
exchanged between and within the atoms comprising the lab. Due to the gradient of rg between
the bottom and top of the lab, the energy exchange in the lab is unbalanced. An atom at the
bottom of the lab emits photons having a lower frequency and energy than the photons it would
emit were it at the top of the lab. =.9999999993054685. Throughout the lab, energy is being
exchanged between and within the atoms comprising the lab. Due to the gradient of rg between
the bottom and top of the lab, the energy exchange in the lab is unbalanced. An atom at the
bottom of the lab emits photons having a lower frequency and energy than the photons it would
emit were it at the top of the lab.
This energy exchange imbalance throughout the lab along lines
to the massive body will be represented by the imbalance in the energy exchanged between an
atom at the bottom of the lab and an atom of the same element at the top of the lab. The
energy of a photon emitted by an atom is a function of the emission frequency and Planck
constant as specified by Eq. (22). The emission frequencies of the photons emitted at the
bottom and top of the lab in Fig. 7 are reduced in proportion to the physical change
ratios, 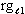 and and 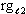 because all processes are
slowed in proportion to rg. Therefore, the energy exchange imbalance (deg) caused by the
gradient of rg between the bottom and top of the lab is as follows. because all processes are
slowed in proportion to rg. Therefore, the energy exchange imbalance (deg) caused by the
gradient of rg between the bottom and top of the lab is as follows.
| | 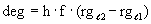 |
(35) |
By substituting the above values of 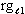 and
and 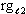 into Eq. (35) the energy exchange imbalance due to the
gradient of rg is deg=h·f·3.26·10-14 joules. The energy
exchange imbalance throughout the lab results in a net force toward the massive body because
the lab's atoms absorb more energy moving downward than energy moving upward. into Eq. (35) the energy exchange imbalance due to the
gradient of rg is deg=h·f·3.26·10-14 joules. The energy
exchange imbalance throughout the lab results in a net force toward the massive body because
the lab's atoms absorb more energy moving downward than energy moving upward.
As shown in Fig. 7, rocket engines exert a force on the lab
which keeps the lab from accelerating toward the massive body. Without this force, the lab
will have an acceleration of 9.8 ma/sa2 or
3.26·10-8 ca/sa toward the massive body. This is the
acceleration of a stone falling to Earth, and it is the acceleration, a, via Eqs. (1) and
(2) if we let m1 be the stone's mass
and m2 be Earth's mass so that
a= F/m1=
m2·G/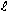 2 =
5.98·1024·2.47·10-36/.0212662. 2 =
5.98·1024·2.47·10-36/.0212662.
(Note: The cause of gravity described above is the gradient in the qm around a massive body
where the speed of light is slower nearer the massive body. A "gravitational force" per se is
unnecessary, and the number of fundamental forces needed to describe nature is reduced to three.)
|
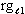 and
and 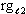 into Eq. (35) the energy exchange imbalance due to the
gradient of rg is deg=h·f·3.26·10-14 joules. The energy
exchange imbalance throughout the lab results in a net force toward the massive body because
the lab's atoms absorb more energy moving downward than energy moving upward.
into Eq. (35) the energy exchange imbalance due to the
gradient of rg is deg=h·f·3.26·10-14 joules. The energy
exchange imbalance throughout the lab results in a net force toward the massive body because
the lab's atoms absorb more energy moving downward than energy moving upward.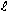 2 =
5.98·1024·2.47·10-36/.0212662.
2 =
5.98·1024·2.47·10-36/.0212662.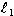 =.021266 LS from the massive body and the top
of the lab is
=.021266 LS from the massive body and the top
of the lab is 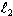 =.021266+10-6 LS
from the massive body. Therefore, a gradient of rg exists in the lab. Using Eq. (33) and
the above values for
=.021266+10-6 LS
from the massive body. Therefore, a gradient of rg exists in the lab. Using Eq. (33) and
the above values for