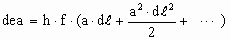|
Apparent equivalence of acceleration and gravity
Now consider the laboratory
in Figure 8 which is at rest in the qm far from any
massive body. At time ta=0 sa rockets on the lab begin exerting an upward force on the
lab which causes an upward acceleration, a. At time ta=0 sa, when the absolute velocity of
the lab is zero, a photon emitted by an atom at the bottom of the lab toward the top of the
lab has an energy which is a function of its velocity relative to the atom from which it was
emitted. This relative velocity varies due to thermal and other motions of the atoms in the
lab, but on average it is 1 ca.
By the time the photon has traveled to where the top of the lab
was at ta=0 sa, its velocity relative to the lab is equal to
(1 - a·10-6) ca. At this time,
ta=10-6 sa, the top of the lab has moved upward a distance of
(a·10-12/2) LS and the photon must travel another
(a·10-12/2) sa to reach this location. During the
(10-6 + a·10-12/2) sa
needed for the photon to reach this location, the lab moves further. By the time the photon
reaches the top of the lab, the lab's absolute velocity is very nearly equal to
va=(a·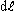 + a2· + a2·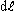 2/2 +
a3· 2/2 +
a3·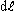 3/2
+ a4· 3/2
+ a4·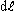 4/8) ca,
where 4/8) ca,
where 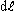 =10-6 LS.
Because =10-6 LS.
Because 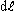 and a are very small numbers, the
velocity of the lab is nearly equal to the first two terms. Thus by the time the photon
reaches the top of the lab, its velocity relative to the lab is approximately
(1 - a·10-6 - a2·10-12/2) ca,
and the photon has been redshifted relative to the lab. and a are very small numbers, the
velocity of the lab is nearly equal to the first two terms. Thus by the time the photon
reaches the top of the lab, its velocity relative to the lab is approximately
(1 - a·10-6 - a2·10-12/2) ca,
and the photon has been redshifted relative to the lab.
Due to this Doppler redshift, when the photon is absorbed at
the top of the lab, the energy that it transfers to the absorbing atom is less than the energy
emitted by the atom at the bottom of the lab. Similarly, a photon emitted at the top of the lab
is blueshifted relative to the lab by the time it reaches the bottom. These red and blueshifts
occur even if the velocity of the lab is not zero at time ta=0. The energy exchange imbalance,
as photons transfer energy between the bottom and top of the lab, is a function of the
magnitude of the red and blueshift. This energy exchange imbalance (dea) caused by
acceleration, is a function of the acceleration, a, the distance, 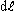 , between the bottom and
top of the lab, the oscillation frequency of the photons, f, and the Planck constant, h, as
follows. , between the bottom and
top of the lab, the oscillation frequency of the photons, f, and the Planck constant, h, as
follows.
| | 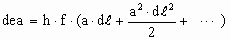 |
(36) |
If we let the acceleration, a, in Eq. (36) be the acceleration
of the lab of Fig. 7 if the rockets are shut down (3.26·10-8 ca/sa), then
dea=h·f·3.26·10-14 joules. This is the same energy exchange imbalance as occurs in Fig. 7,
where deg=h·f·3.26·10-14 joules according to Eq. (35) due to the gradient of rg in the
laboratory. Because deg, the energy exchange imbalance in Fig. 7, is equal to dea, the
energy exchange imbalance in Fig. 8, the force of the rockets on the lab in Fig. 7
must equal the force on the lab in Fig. 8. Inside the labs the effect of the acceleration
in Fig. 8 is the same as the effect of "gravity" in Fig. 7, which makes it appear to
observers(c) that the phenomena are equivalent.
If the rockets in Fig. 7 are shut down, the energy exchange
imbalance inside the lab due to the gradient of rg causes an acceleration of the lab
sufficient to balance the energy exchange via Doppler shifts of the lab's wave/particle energy.
According to the quantum medium view, an apple hanging on a tree has an internal energy
exchange imbalance, and if Newton observed an apple falling to Earth, he was observing the
balancing of the apple's internal energy exchange via the apple's acceleration.
|
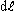 + a2·
+ a2·