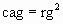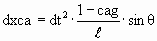|
Propagation of light in the vicinity of a massive body
In accordance with Premise II and experimental evidence, it is
assumed that the speed of light, cag, at a particular location in the qm is a simple function
of rg at that location as follows.
| | 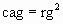 |
(37) |
It is also assumed that the gradient of rg and cag around a
massive body causes a bending of the path of a wave/particle quanta of energy toward the
massive body according to Eq. (38) and
Figure 9.
| | 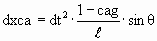 |
(38) |
For example, during a small time increment (dt) sa, a photon, p, which is
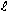 LS from a massive body of m kga, has a velocity, cag, specified
by Eqs. (33) and (37). The photon moves a distance of cagˇdt LS with an initial
trajectory at angle θ to a line to the massive body, as shown in Fig. 9. The photon
also has a component of motion, dxca specified by Eq. (38), at right angles to its initial
trajectory and toward the massive body, as shown. These two components of motion specify the
photon's location, p', at the end of the time increment. A line from p through p' specifies
the initial trajectory angle for the next time increment. Using this step-and-repeat process,
a photon's motion through a gradient of rg in the qm can be computed. LS from a massive body of m kga, has a velocity, cag, specified
by Eqs. (33) and (37). The photon moves a distance of cagˇdt LS with an initial
trajectory at angle θ to a line to the massive body, as shown in Fig. 9. The photon
also has a component of motion, dxca specified by Eq. (38), at right angles to its initial
trajectory and toward the massive body, as shown. These two components of motion specify the
photon's location, p', at the end of the time increment. A line from p through p' specifies
the initial trajectory angle for the next time increment. Using this step-and-repeat process,
a photon's motion through a gradient of rg in the qm can be computed.
Simple equations (33), (37), and (38) are consistent with
experimental evidence that has been cited to support general relativity theory. We will
compare consequences of these equations with the experimental evidence.
|
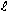 LS from a massive body of m kga, has a velocity, cag, specified
by Eqs. (33) and (37). The photon moves a distance of cagˇdt LS with an initial
trajectory at angle θ to a line to the massive body, as shown in Fig. 9. The photon
also has a component of motion, dxca specified by Eq. (38), at right angles to its initial
trajectory and toward the massive body, as shown. These two components of motion specify the
photon's location, p', at the end of the time increment. A line from p through p' specifies
the initial trajectory angle for the next time increment. Using this step-and-repeat process,
a photon's motion through a gradient of rg in the qm can be computed.
LS from a massive body of m kga, has a velocity, cag, specified
by Eqs. (33) and (37). The photon moves a distance of cagˇdt LS with an initial
trajectory at angle θ to a line to the massive body, as shown in Fig. 9. The photon
also has a component of motion, dxca specified by Eq. (38), at right angles to its initial
trajectory and toward the massive body, as shown. These two components of motion specify the
photon's location, p', at the end of the time increment. A line from p through p' specifies
the initial trajectory angle for the next time increment. Using this step-and-repeat process,
a photon's motion through a gradient of rg in the qm can be computed.