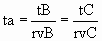Agreement among observers in different reference frames
     Special relativity theory is based on two postulates reflecting the experimental evidence. The first postulate says that the laws of physics are valid in all inertial reference frames. The second says that the speed of light, c, is the same in all inertial reference frames. This second postulate results in observers in different reference frames having different standards of distance and time, for reasons discussed above. Therefore, the observers cannot agree on the dimensions of bodies, the rates of clocks, and the order in which events occur.
     Although the first postulate of special relativity is reasonable, is it not also reasonable that the laws of physics should permit observers in different reference frames to agree on what is occurring in nature and to explain in a logical way why it is occurring? As a consequence of Premise I of the quantum medium view, observers in different inertial reference frames agree on the lengths, clock rates, time intervals, and order of events they observe when they agree on an absolute reference frame. Even if their assumed absolute reference frame has a velocity through the qm that is small relative to ca, observers in different reference frames will be in complete agreement on all the phenomena they observe, and the observed phenomena will be very close to the real, absolute phenomena occurring in the medium.
     We will distinguish between two kinds of observers who make fundamentally different assumptions about light, and we will refer to them as observers(c) and observers(cr). Observers(c) assume that the speed of light is constant, c, in all inertial reference frames. Observers(cr) assume that light is propagated through a medium and that the speed of light, cr, is not constant relative to an inertial reference frame moving through the medium.
     Figure 3 shows inertial reference frames B and C moving relative to one another and relative to an agreed-upon absolute reference frame A at rest in the qm. Each axis of each reference frame has distance marks (not shown) which are 1 ma apart when at rest in the qm. In B and C the marks along the Bx and Cx axes are closer together, for reasons explained previously (just as the .1 ls marks on the x axis of reference frame B in Fig. 1 are closer together than when B is at rest in the qm). Each distance mark has a clock which is synchronized with all the other clocks in its coordinate system, as explained below.
     Observers(cr) in reference frames B and C can determine their real, absolute velocities, vBa and vCa, by observing the absolute distance marks and clocks on the Ax axis as the origins of their coordinate systems pass the marks and clocks. The observers(cr) in A, B, and C know that all clocks and distance scales in A indicate real times and distances. Also, every observer knows the real speeds of light between any two locations in any system. For example, in B the speeds of light moving parallel to the x axis are (1+vBa) ca and (1-vBa) ca, and for light moving along lines parallel to the y or z axes the speed is rvB ca. In system A the speed of light is always 1 ca.
     All observers(cr) know, via Eq. (8), the physical change ratios for systems B and C.

Every observer knows that in B and C every clock is slowed and all distance scales are foreshortened in the direction of absolute motion in proportion to the physical change ratio for the system. Thus all observers can convert all clock and distance scale readings into absolute units, regardless of the coordinate systems of the observers, clocks, or distance scales.
     All observers know that an absolute second, 1 sa, is a time duration equal to 1 s on an atomic clock in A (or rv s on any atomic clock, where rv is the clock's physical change ratio). An absolute time (ta) specifies the time in absolute seconds, sa, before (-) or after (+) a particular event occurs. At time ta=0 sa, the origins of A, B, and C were coincident and the origin clocks read 0 s. Because every observer in the three coordinate systems knows the speed of light from the clock at the origin of her coordinate system to her clock, she can really synchronize her clock with the origin clock. Therefore, within each system, all clocks in the system are synchronized.
     At time ta=0 sa, all clocks in the three coordinate systems read zero. At time ta, all clocks in A read ta, but all clocks in B read tB and all clocks in C read tC. Every clock in B and C has been slowed in proportion to its physical change ratio as follows.

and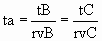

(17)

     Because observers(cr) in B and C can determine absolute times and distances, they can determine the absolute velocity of C relative to B, vCBa. Absolute velocities add in the classical way as follows.

     The absolute distances between the origins of the coordinate systems, ABa, ACa, and BCa depend on the absolute velocities and absolute time.

The absolute distances add in the classical way.

     At time, ta, event E occurs at location (Axa, Aya, Aza). In system B the event occurs at location (Bxa, Bya, Bza), and in system C it occurs at (Cxa, Cya, Cza), where these absolute distances are related to the labeled distances on the axes of the coordinate systems as follows.

That is, Bxa, Bya, and Bza are the absolute distances of the event along the Bx, By, and Bz axes, and Bx, By, and Bz are the labeled distances on the axes at real distances Bxa, Bya, and Bza.
     All observers(cr) in all the coordinate systems therefore know the absolute location of any event and the absolute time of the event. Consequently, all observers(cr) agree on the absolute time durations between different events, and the observers agree on the order of the events.
     Therefore, all observers(cr) in A, B, and C use the same absolute units of time and distance and they all agree on the phenomena occurring in the qm. They do not need to make transformations between the observations made in one reference frame and the observations made in other reference frames because the observations are the same in all the reference frames.