Natural Shape of the Chambered Nautilus Shell
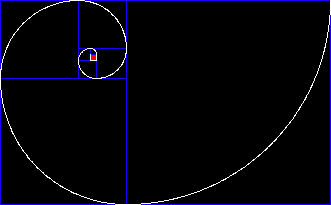
      Imagine a family raising sheep on a remote prairie. Initially the sheep are kept in a square fenced area at night where they are safe from predators and where the family sleeps and keeps supplies. This initial "compound" is 1 chain square, which is about 20x20 meters, and at one corner it has a gate extending several meters along one side. It is shown by the little red box in the left figure above. By and by the sheep multiply and outgrow this first area, and a second area (orange) is attached to the gated side of the first. As the herd grows, increasingly large square areas are added using the long side of the existing compound that is closest to the initial gate and compound. Following this simple rule for enlarging the fenced area, the compound grows to the size shown.

      This natural growth procedure, which produces increasingly large rectangles, has interesting consequences. As the rectangles get larger, the ratio of width to length gets closer and closer to 0.61803398874 ... which is the remarkable "golden ratio" known to ancient Greeks. In the above case, the ratios for the eight rectangles are as follows: 1/2=.500, 2/3=.666, 3/5=.600, 5/8=.625, 8/13=.615, 13/21=.619, 21/34=.617, and 34/55=.618. Even if the initial compound is a rectangle rather than a square, the compound will always grow toward the golden rectangle shape.

      If fencing were essential and costly, families would find that they could enlarge their compounds more efficiently if they made the additions using 1/4 circle fence additions as shown in the middle figure. This requires less fencing and labor, and the corner areas cut off by the curved fence will still be within the compound after a few more enlargements. Thus the fences of the compounds would be spirals - - which brings us back to the chambered nautilus, which also has a need for protection and uses an instinctive spiral growth strategy that has survived because it's efficient and effective.

      The nautilus shell and endless other wonderful things in nature seem mysterious until reasons behind their existences become apparent. And often the reasons are even more amazing than the observed phenomena. But how are people involved in day to day activities going to appreciate that things and events can be traced back to underlying causes? Newton's remark, "God created everything by number, weight and measure," is a good guide to keep in mind as we try to make sense of nature and life.