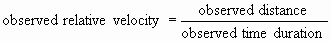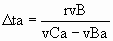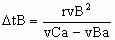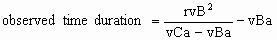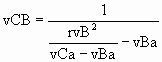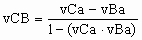|
Observed virtual relative velocity
It was shown above why the observers in reference frames A
and B of Fig. 1 determined that the observed velocity of B relative to A (vBA)
was .6 c. The observers divided an observed distance moved through their reference frame
by the observed time duration.
| 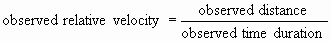 |
(9) |
We will now generalize what the observed relative velocity will
be for the observers when both reference frames are moving through the qm. Two reference frames,
B and C, are shown in Figure 2. The absolute
velocity of B (vBa) and the absolute velocity of C (vCa) are in the x direction. It
will become apparent that the absolute velocity of C relative to B (vCBa) is not the
same as the virtual relative velocity observed in B and C (vCB).
We will simplify this derivation of vCB by having the observed
distance in the observer's reference frame be 1 ls so that Eq. (9) becomes the
following.
|  |
(10) |
In reference frame B a 1 ls distance along the x axis is
equal to an absolute distance of rvB LS, where rvB is the physical change
ratio for B. This absolute distance, divided by the absolute velocity of C relative to B
is equal to the absolute time duration (Δta) for C to move 1 ls along
the x axis of B.
| 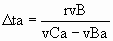 |
(11) |
During this absolute time duration, Δta sa, clocks in B advance rvB·Δta or
ΔtB s as follows.
| 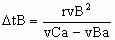 |
(12) |
The clock located at the end of the observed 1 ls distance in B is out of synchronization
with the clock at the beginning by -vBa s (according to the asynchronization RULE above).
This asynchronization is added to ΔtB of Eq. (12) to obtain the observed time
duration as follows.
| 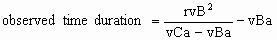 |
(13) |
Combining Eqs. (10) and (13) yields the following.
| 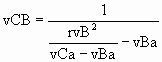 |
(14) |
Via Eq. (8), rvB2=1-vBa2.
Therefore, Eq. (14) can be modified to Eq. (15) in which the observed virtual relative
velocity is a function of the absolute velocities of reference frames B and C.
| 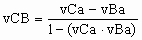 |
(15) |
Following the above procedure for Eqs. (11) through (15), we
could show that observers in C, using the clocks and distance marks in their reference frame,
will observe the same relative velocity, vCB, specified by Eq. (15).
When the absolute velocity of one of the reference frames is zero,
Eq. (15) becomes vCB=vCa-vBa. Therefore, in Fig. 1 where reference frame A is at rest
in the qm, the observers in A and B determine that their relative velocity is vBA=.6 c,
the same value as the absolute velocity of B relative to A, vBAa=.6 ca. The rationale
behind Eq. (15) helps explain why a body will not be observed traveling faster than the
speed of light through the observer's reference frame. In Fig. 1, if a body has an
absolute velocity of .9 ca in the -x direction, it has a velocity of 1.5 ca through
reference frame B, but in B it is observed that the body has a velocity of .97 c through B.
|