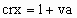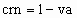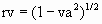Consequences of the qm in inertial reference frame B
     An obvious consequence of the medium is that the speed of light, cr, is not constant relative to any reference frame moving through the medium. In any inertial reference frame, the maximum speed of light (crx) and the minimum speed of light (crn) depend on the absolute velocity, va, of the reference frame as follows.

(5)

(6)

     Therefore, in reference frame B, crx=1.6 ca and crn= .4 ca because va=.6 ca. Along the x axis of B, cr is either crx or crn as shown. Along the y and z axes, cr is .8 ca as shown because photons moving along the y and z axes must have a +x direction component of their 1 ca velocity through the medium equal to .6 ca.
     Because photons moving in the y and z directions of B have a velocity of only .8 ca relative to B, the rate of photon exchange in the y and z directions of B is only .8 times the at-rest rate. The term, at-rest, means when a reference frame or body is not moving through the qm. It will soon become apparent why the round-trip rate of photon exchange along the x axis of B is also .8 times the at-rest rate.
     The rate of round-trip energy exchange within any inertial reference frame moving through the qm relative to the at-rest rate is proportional to the physical change ratio (rv) for the reference frame. This physical change ratio, rv, is a function of crx and crn (or va) as follows.

(7)

(8)

Therefore, in reference frame B, rv=.8 because crx=1.6, crn=.4 and va=.6. All processes in B are slowed in proportion to rv, including the rate of energy exchange between atoms and within atoms, the rate of vibration of atoms, the rate of radioactive decay and muon decay (assuming that muons are dynamic systems within which energy is transferred via the qm), and the rate of clocks. (It will be shown below why the rate of a simple mechanical clock in B is slower than its at-rest rate.) A second displayed on a clock in B is a virtual second (s) . In any inertial reference frame moving through the medium a virtual second displayed on a clock is equal to a time duration of 1/rv absolute seconds. Therefore, 1 s on a clock in B is 1.25 sa. (In reference frame A, rv=1 because va=0, and 1 s on a clock is 1 sa.)
     Observers in reference frame B put distance marks at the 1 light-second locations, just as was done in A. On the y and z axes the 1 light-second marks are 1 LS from the origin due to "offsetting errors." The observers are unaware that the speed of light along y and z is only .8 ca, and they are also unaware that the 2 s round-trip travel time shown on their clocks is 2.5 sa. On the x axis the observer at the 1 light-second location also allows 2 s on her clock for the round-trip light signal to travel to the origin and back. This 2.5 sa time duration results in placing the 1 light-second mark only .8 LS from the origin. (The light signal traveling to the origin at cr=1.6 ca takes .5 sa, and the return signal traveling at cr=.4 ca takes 2 sa.)
     Distances marked off by observers in B are virtual distances in virtual light-second (ls) units which are the result of the observers using virtual seconds, s, and the virtual constant speed of light, c. Along the y and z axes the virtual distances are the same as the absolute distances. Along the x axis the distances marked in B are rv (or .8) times the distances marked in A as shown. Observers in B believe that the 1 ls distance along x is exactly the same distance as the 1 ls distances along y and z. The observed rates of energy exchange along the three axes in B are balanced when the distances marked along x are rv times the distances marked along y and z.
     The rates of energy exchange between atoms and within atoms in a body at rest relative to reference frame B are also balanced when distances between the atoms and within the atoms in the x direction are rv times the distances in the y and z directions. For this and other reasons, a body in B is only rv times as long in the x direction as it would be in reference frame A. A meter stick, which has an at-rest length of 1 absolute meter (ma), is only .8 ma long when oriented parallel to the x axis in B, but in B it is observed that the length of the meter stick is 1/(3·10⁸) ls or 1 meter (m). If the meter stick is then rotated 90° and oriented parallel to the y axis, its length increases to 1 ma, but in B it is still observed to be 1 m long.
     Clocks in B are virtually synchronized by observers at the distance marks (following the same procedure as observers in A). At time tA=1 s (when reference frames A and B are as shown in Fig. 1), observers at the 1 ls locations on the y and z axes in B see the origin clock as it was 1.25 sa earlier (or 1 s earlier on clocks in B) when the origin clock displayed -.2 s. Thus these observers believe that their clocks should display .8 s as shown in Fig. 1.
     Clocks along the x axis of B are out of sync as shown. The observer at the 1 ls mark sees the origin clock as it was 2.0 sa earlier (when it displayed -.8 s) because it takes 2.0 sa for light from the origin to travel the .8 LS distance to the 1 ls mark. The observer, allowing for her 1 ls distance from the origin, has her clock displaying .2 s as shown.
     RULE: In any inertial reference frame moving through the medium, two clocks are out of sync by an amount equal to the absolute velocity of the reference frame times the observed distance between the clocks in the direction of absolute motion. The forward clock is set retarded relative to the rearward clock. (Therefore, clocks on the y and z axes in B are synchronized.)
     The laws of physics appear to observers in B to be valid, but the laws describe virtual phenomena because the units of time, distance, mass, etc. in B are virtual units.
     Among the relativistic, virtual phenomena observed in B is the 1 light-second distance marked on the x axis of reference frame A. Observers in B determine that this 1 LS distance is only .8 times the 1 ls distance marked on the x axis of B. The observers also determine incorrectly that the rate of clocks in reference frame A is .8 times the rate of clocks in reference frame B. The observers also determine that the velocity of B relative to A is .6 c. This observed velocity is the result of offsetting errors in observed time and observed distance in B.