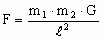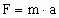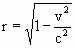|
Background
Similarly, a body's inertia or resistance to being accelerated by a force is specified by Newton's second law of motion and Eq. (2) where a force, F, on a body of mass, m, results in an acceleration, a, of the body.
Similarly, the observed "relativistic" effects of motion between bodies and observers seem mysterious even though they are specified by Albert Einstein's special theory of relativity. If two identical spaceships, each with a clock and an observer, travel from Earth into remote space and then move past one another with observed relative velocity, v, each observer will find that the clock on the other spaceship is running slower than the observer's clock. The ratio, r, of the observed rate of the other clock to the rate of the observer's clock is specified by the following equation.
Equation (3) says that when the two spaceships are parked next to one another so that v =0 and r =1, the observers agree that the clocks run at the same rate. But if spaceship A moves away from ship B and then returns with a high velocity relative to B, the observer on A will find that the clock aboard B is running slower than clock A, and observer B will find that clock A is running slower than clock B. What could be the physical causes of this strange phenomenon? Why should changing the velocity of ship A affect the rate of the clock aboard ship B? It will be shown why a change in the velocity of ship A causes physical changes aboard ship A and causes the relativistic phenomena observed aboard both ships. It will also be evident that observers A and B can agree on the rates of the clocks and the lengths and masses of the ships if the observers are aware of the physical causes of the relativistic phenomena. Relativity theory assumes that the speed of light is always the same for all observers, an assumption that gained acceptance because it is consistent with experimental observations. Observers aboard a spaceship will determine that the photons from a distant star arrive with the same speed, c, relative to the ship whether the ship is moving at high velocity toward the star or at high velocity away from the star. When the spaceship is moving at high velocity toward the star, shouldn't the photons from the star be moving faster relative to the ship? The observed Doppler blueshift due to the ship's velocity toward the star indicates that the photons are moving faster relative to the ship. Then why don't observers aboard the ship detect the higher relative velocity?
|
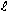 . The universal
gravitational constant, G, was found experimentally to be
6.67·10-11N·m2/kg2.
It relates the force (in newtons) to the masses (in kilograms) and the distance
(in meters).
. The universal
gravitational constant, G, was found experimentally to be
6.67·10-11N·m2/kg2.
It relates the force (in newtons) to the masses (in kilograms) and the distance
(in meters).